Central limit theorem | Wikipedia audio article - YouTube Subhajit Sahu

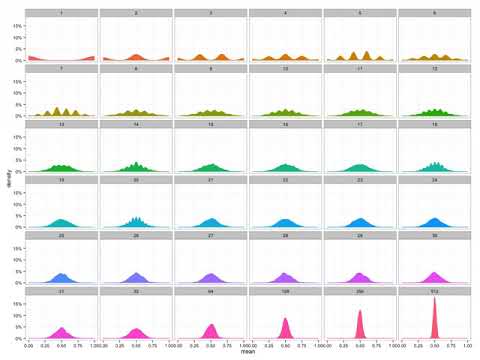
This is an audio version of the Wikipedia Article: https://en.wikipedia.org/wiki/Central... 00:03:17 1 Independent sequences 00:03:28 1.1 Classical CLT 00:06:14 1.2 Lyapunov CLT 00:08:44 1.3 Lindeberg CLT 00:12:57 1.4 Multidimensional CLT 00:15:47 1.5 Generalized theorem 00:33:59 2 Dependent processes 00:34:46 2.1 CLT under weak dependence 00:34:56 2.2 Martingale difference CLT 00:36:05 3 Remarks 00:38:13 3.1 Proof of classical CLT 00:41:21 3.2 Convergence to the limit 00:41:27 3.3 Relation to the law of large numbers 00:41:37 3.4 Alternative statements of the theorem 00:44:20 3.4.1 Density functions 00:51:12 3.4.2 Characteristic functions 00:53:49 3.5 Calculating the variance 01:01:43 4 Extensions 01:01:54 4.1 Products of positive random variables 01:02:58 5 Beyond the classical framework 01:03:59 5.1 Convex body 01:11:07 5.2 Lacunary trigonometric series 01:11:16 5.3 Gaussian polytopes 01:12:31 5.4 Linear functions of orthogonal matrices 01:13:11 5.5 Subsequences 01:13:40 5.6 Random walk on a crystal lattice 01:15:28 6 Applications and examples 01:20:04 6.1 Simple example 01:20:08 6.2 Real applications 01:20:19 7 Regression 01:22:21 7.1 Other illustrations 01:23:53 8 History 01:24:56 9 See also 01:25:22 10 Notes 01:26:09 11 References 01:26:36 12 External links 01:26:47 Simple example 01:27:42 Real applications 01:29:33 Regression 01:30:30 Other illustrations 01:30:54 History 01:37:26 See also Listening is a more natural way of learning, when compared to reading. Written language only began at around 3200 BC, but spoken language has existed long ago. Learning by listening is a great way to: - increases imagination and understanding - improves your listening skills - improves your own spoken accent - learn while on the move - reduce eye strain Now learn the vast amount of general knowledge available on Wikipedia through audio (audio article). You could even learn subconsciously by playing the audio while you are sleeping! If you are planning to listen a lot, you could try using a bone conduction headphone, or a standard speaker instead of an earphone. Listen on Google Assistant through Extra Audio: https://assistant.google.com/services... Other Wikipedia audio articles at: https://www.youtube.com/results?searc... Upload your own Wikipedia articles through: https://github.com/nodef/wikipedia-tts Speaking Rate: 0.7097363357272883 Voice name: en-US-Wavenet-E "I cannot teach anybody anything, I can only make them think." - Socrates SUMMARY ======= In probability theory, the central limit theorem (CLT) establishes that, in some situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution (informally a "bell curve") even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions. For example, suppose that a sample is obtained containing a large number of observations, each observation being randomly generated in a way that does not depend on the values of the other observations, and that the arithmetic mean of the observed values is computed. If this procedure is performed many times, the central limit theorem says that the distribution of the average will be closely approximated by a normal distribution. A simple example of this is that if one flips a coin many times the probability of getting a given number of heads in a series of flips will approach a normal curve, with mean equal to half the total number of flips in each series. (In the limit of an infinite number of flips, it will equal a normal curve.) The central limit theorem has a number of variants. In its common form, the random variables must be identically distributed. In variants, convergence of the mean to the normal distribution also occurs for non-identical distributions or for non-independent observations, given that they comply with certain conditions. The earliest version of this theorem, that the normal distribution may be used as an approximation to the binomial distribution, is now known as the de Moivre–Laplace theorem. In more general usage, a central limit theorem is any of a set of weak-convergence theorems in probability theory. They all express the fact that a sum of many independent and identically distributed (i.i.d.) random variables, or alternatively, random variables with specific types of dependence, will tend to be distributed according to one of a small set of attractor distributions. When the variance of the i.i.d. variables is finite, the attractor distribution is the normal distribution. In contrast, the sum of a number of i.i.d. random variables with power law tail distributions decreasing as |x|−α − 1 where 0 α 2 (and the ...

Central limit theorem | Wikipedia audio article - YouTube
1 Likes	1 Dislikes
14 views views	283 followers
Education Creative Commons Attribution licence (reuse allowed)	Upload TimePublished on 27 Dec 2018